A soliton of Burgers' equation?
A soliton of Burgers' equation?
Burgers-swept KdV Equation: Soliton and Bore Interaction in Shallow Water
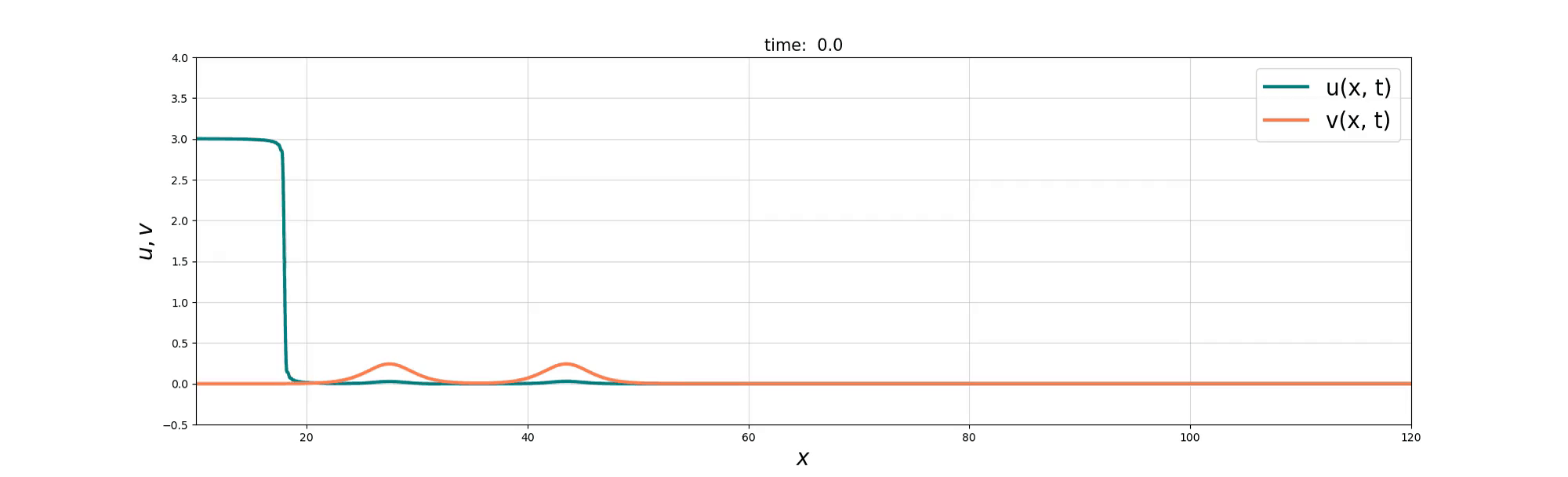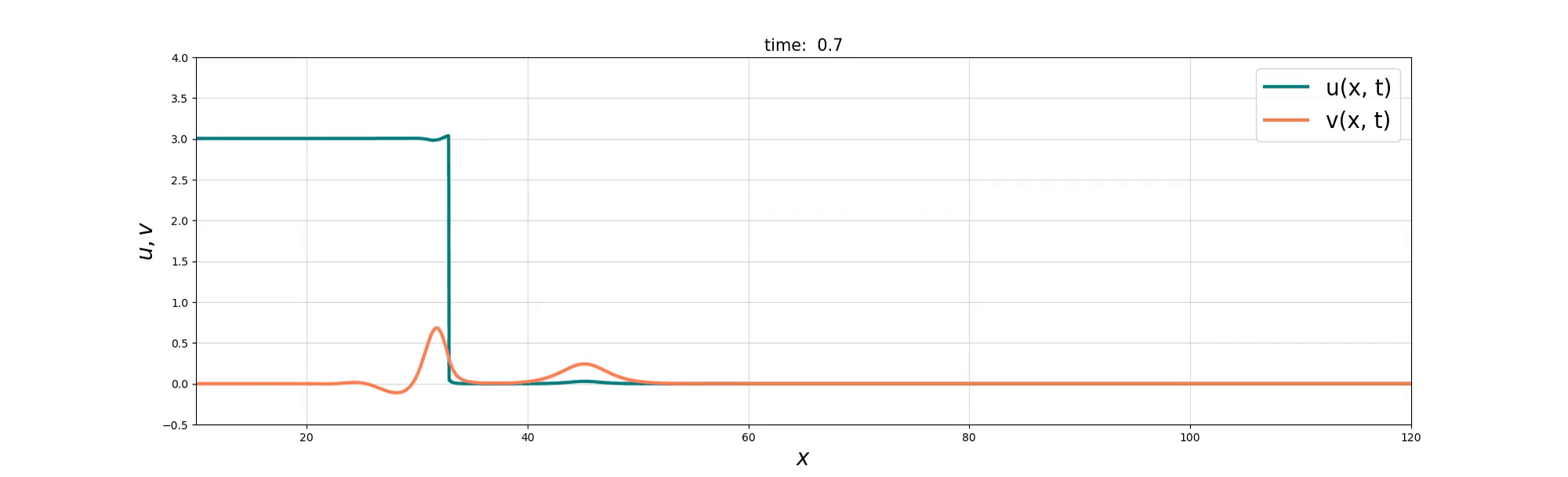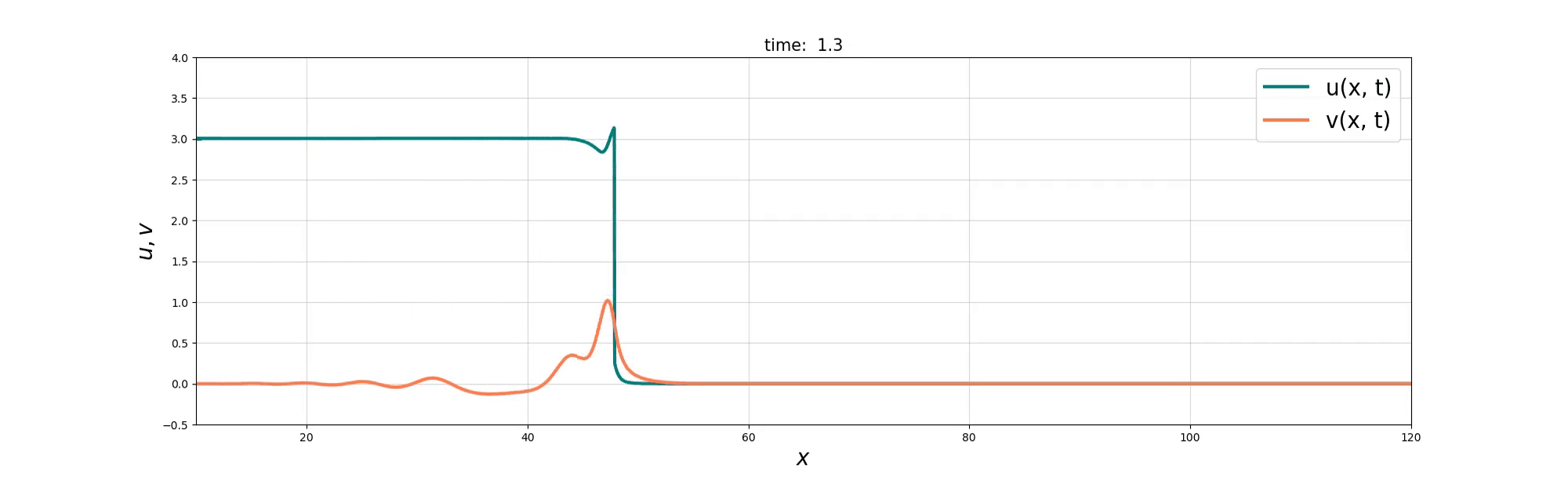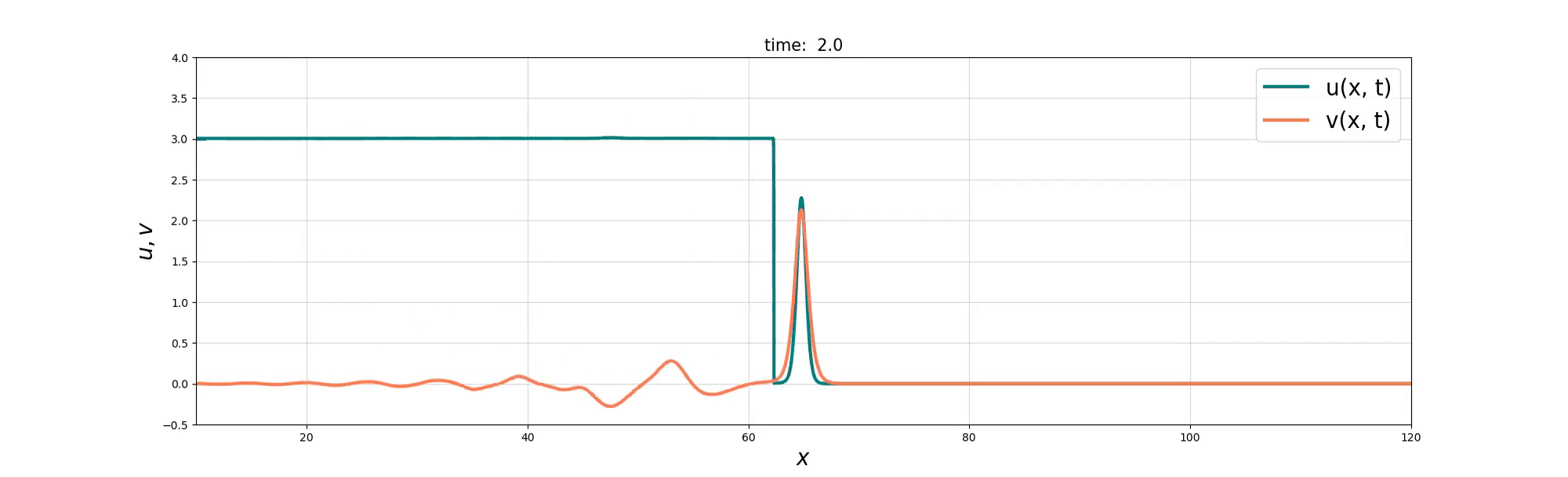
We consider a coupled PDE system between the Burgers equation and the KdV equation to model the interactions between ‘bore’-like structures and wave-like solitons in shallow water. Two derivations of the resulting Burgers–swept KdV system are presented, based on Lie group symmetry and reduced variational principles. Exact compound soliton solutions are obtained, and numerical simulations show that the Burgers and KdV momenta tend toward a balance at which the coupled system reduces to the integrable Gardner equation. The numerical simulations also reveal rich nonlinear solution behaviours that include refraction, reflection, and soliton fusion, before the balance is finally achieved.
$\mathrm{Burgers}: \quad u_t+3 u u_x \quad=-v \partial_x\left(3 v^2+\gamma v_{x x}\right)$,
$\mathrm{KdV}: \quad v_t+6 v v_x+\gamma v_{x x x}=-\partial_x(u v)$.
Or equivalently,
Gardner: $\quad v_t+6 v v_x+\frac{3}{2} v^2 v_x+\gamma v_{x x x}=-\partial_x(v m)$,
Lie Transport: $\quad m_t+\left(m \partial_x+\partial_x m\right) u=0, \quad$ with $\quad m:=u-\frac{1}{2} v^2$,
Soliton Emergence
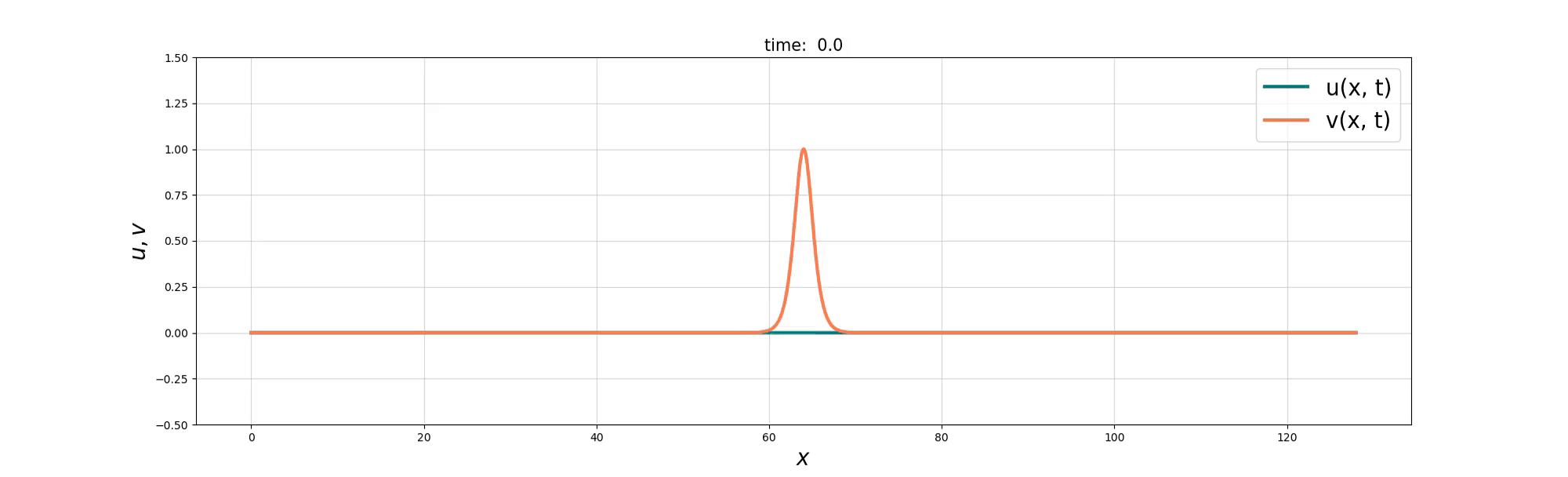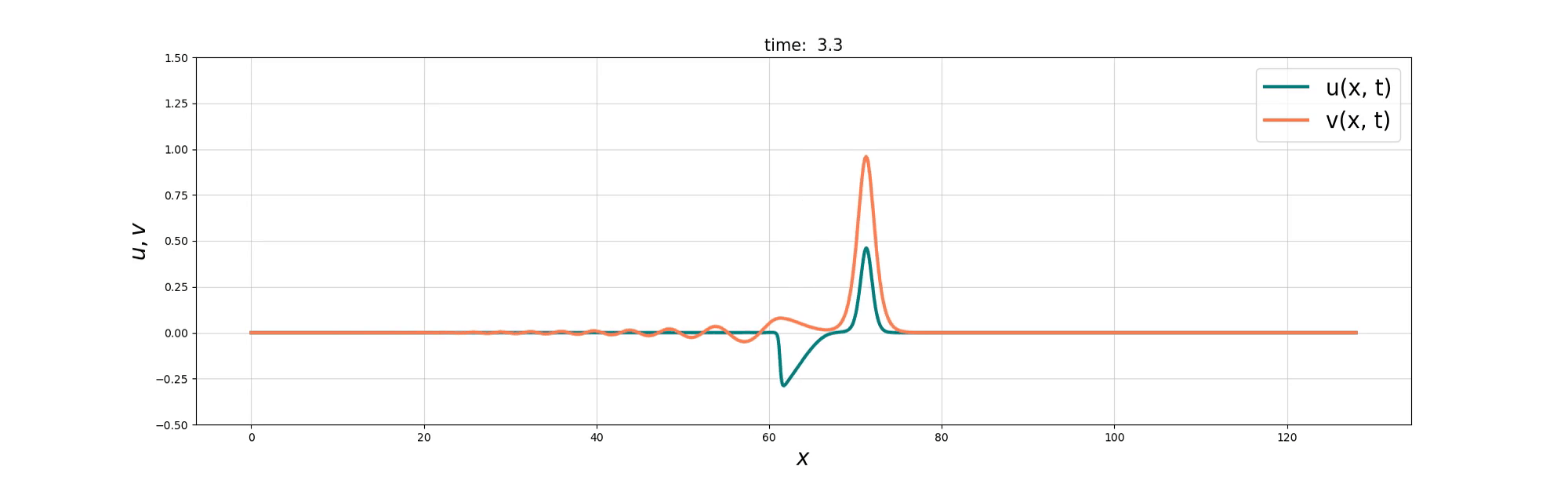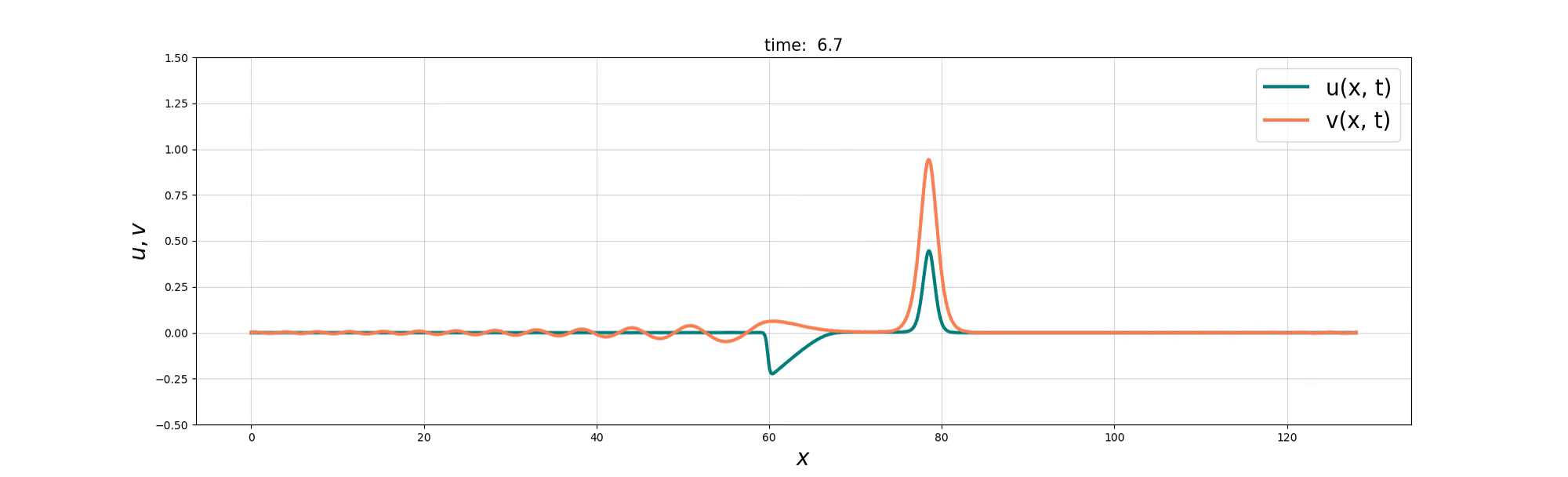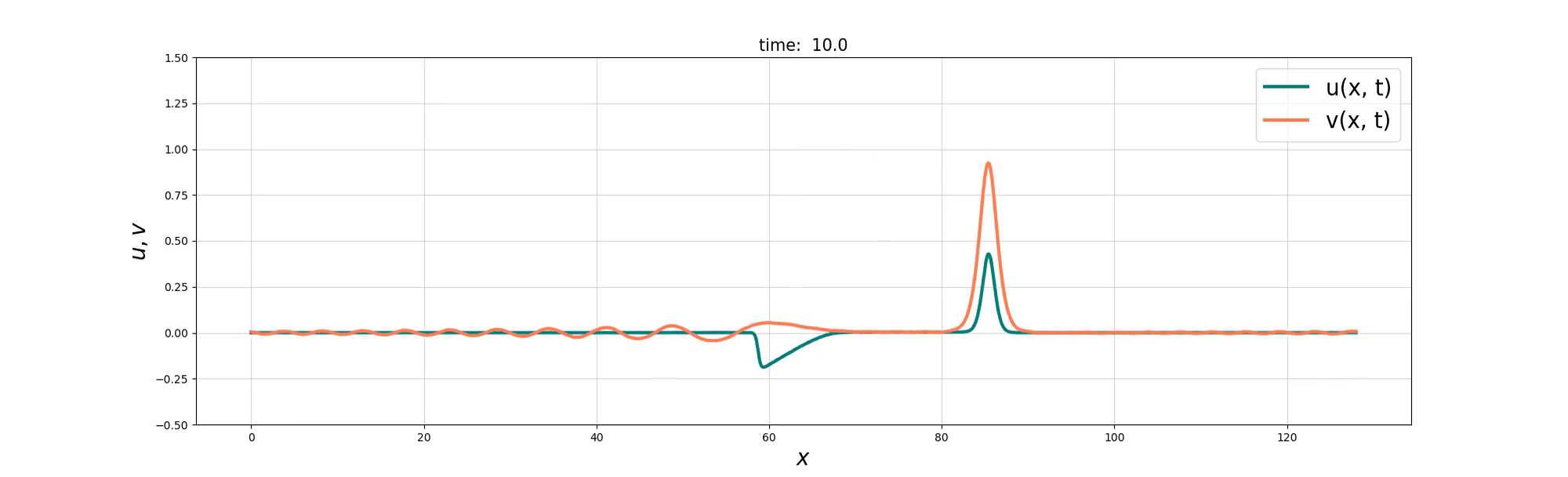
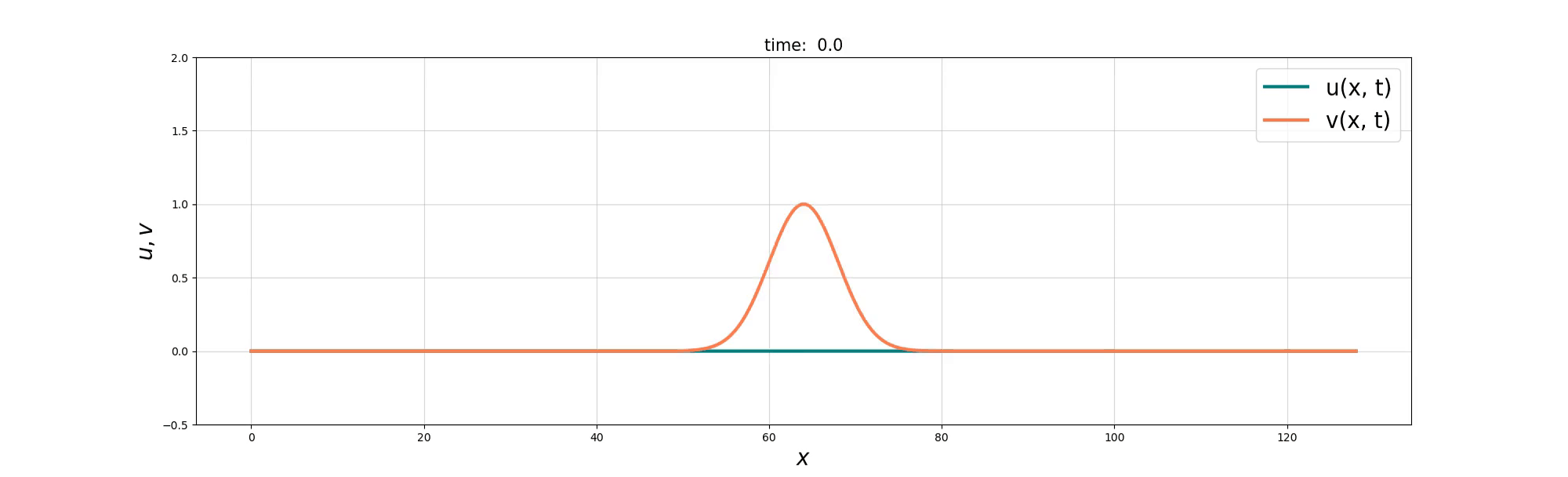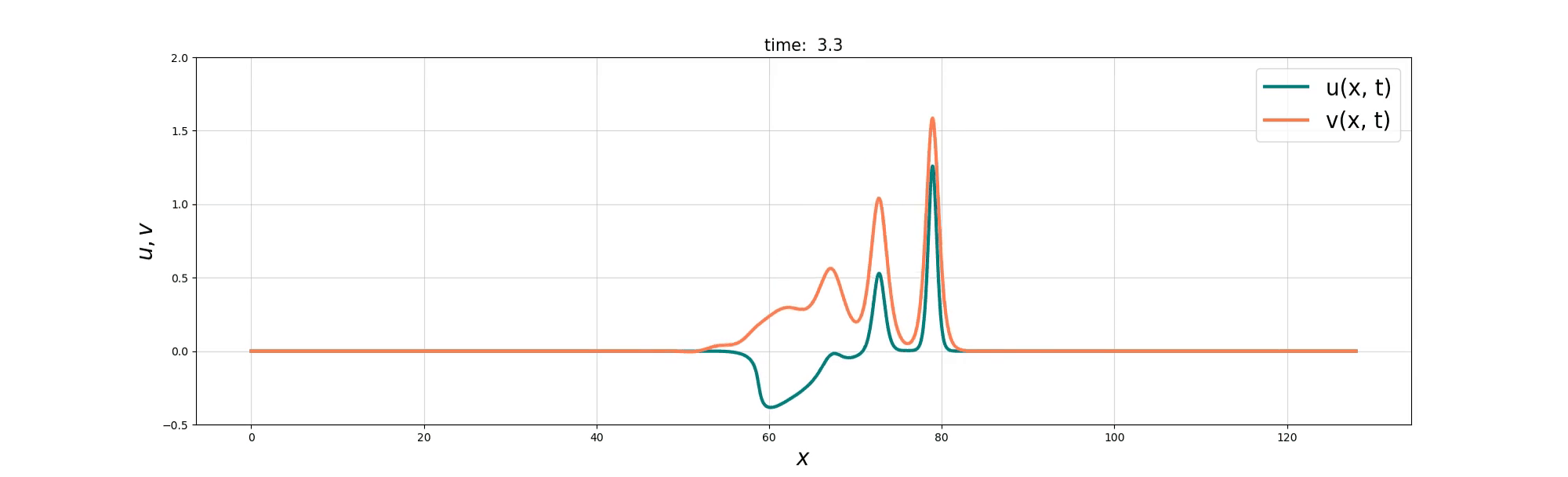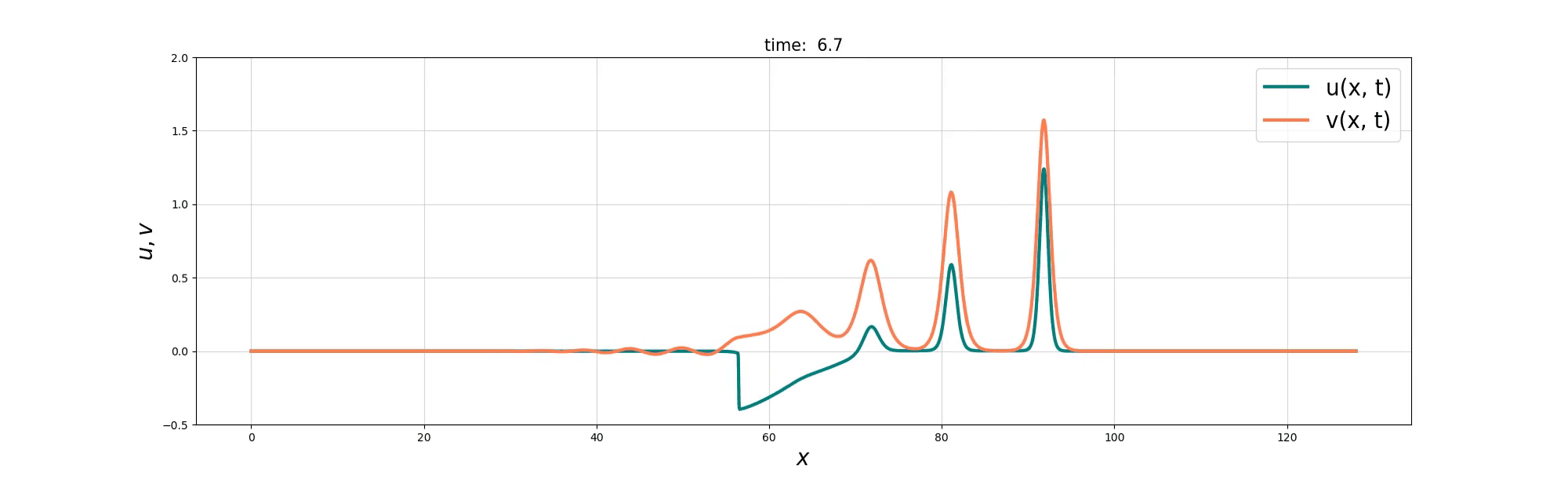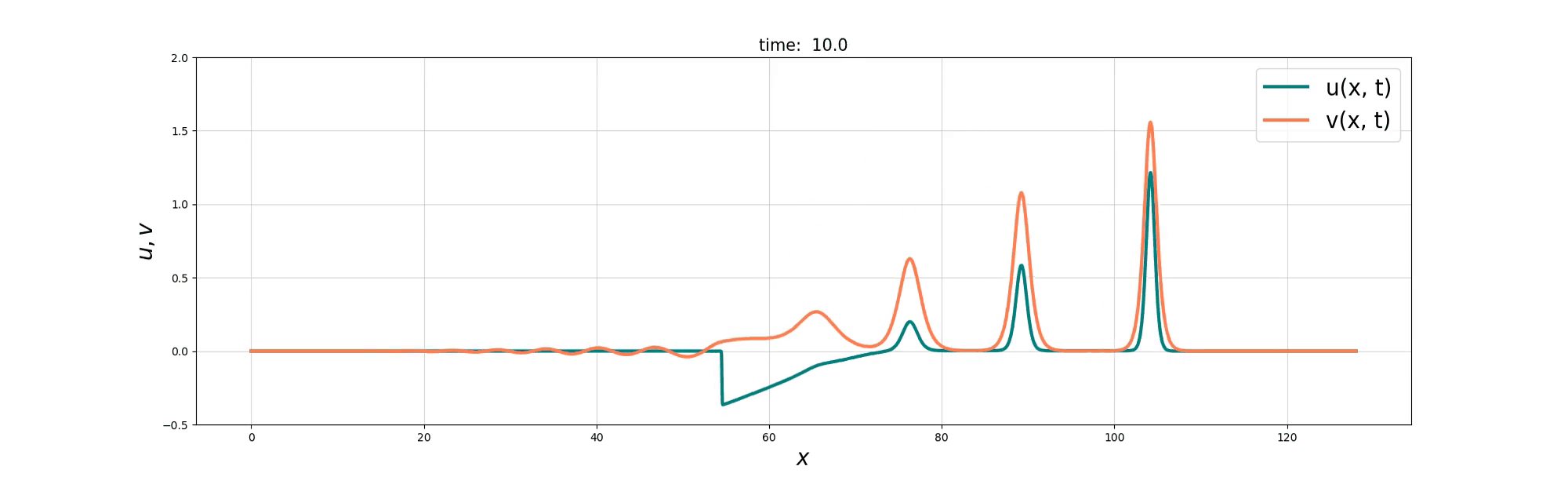
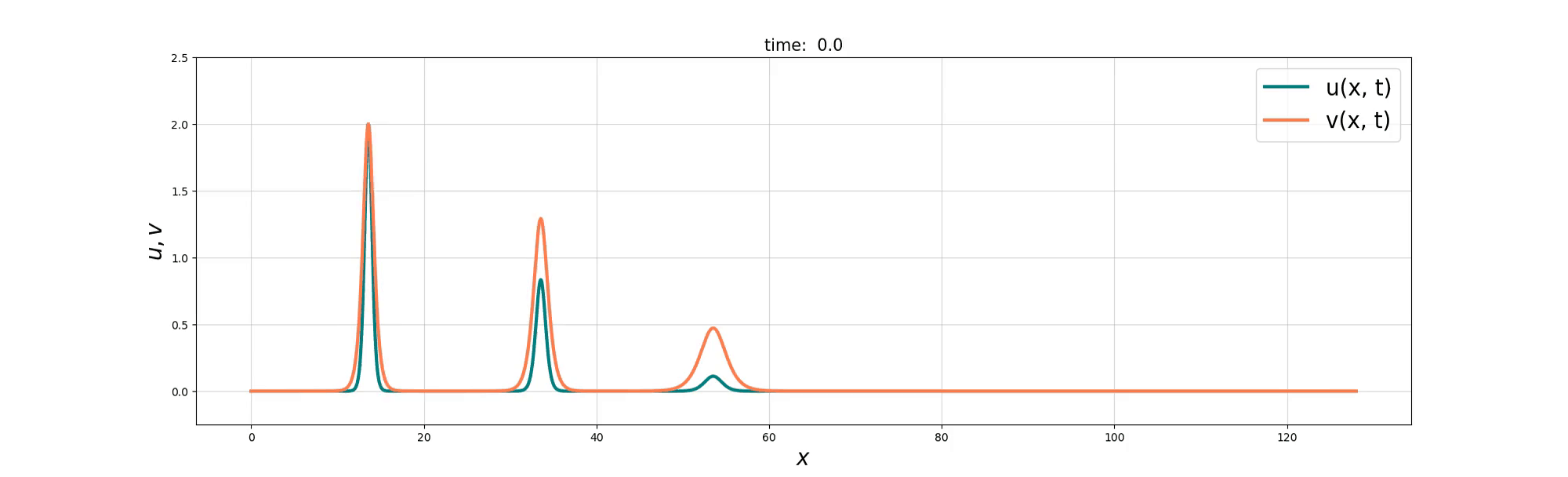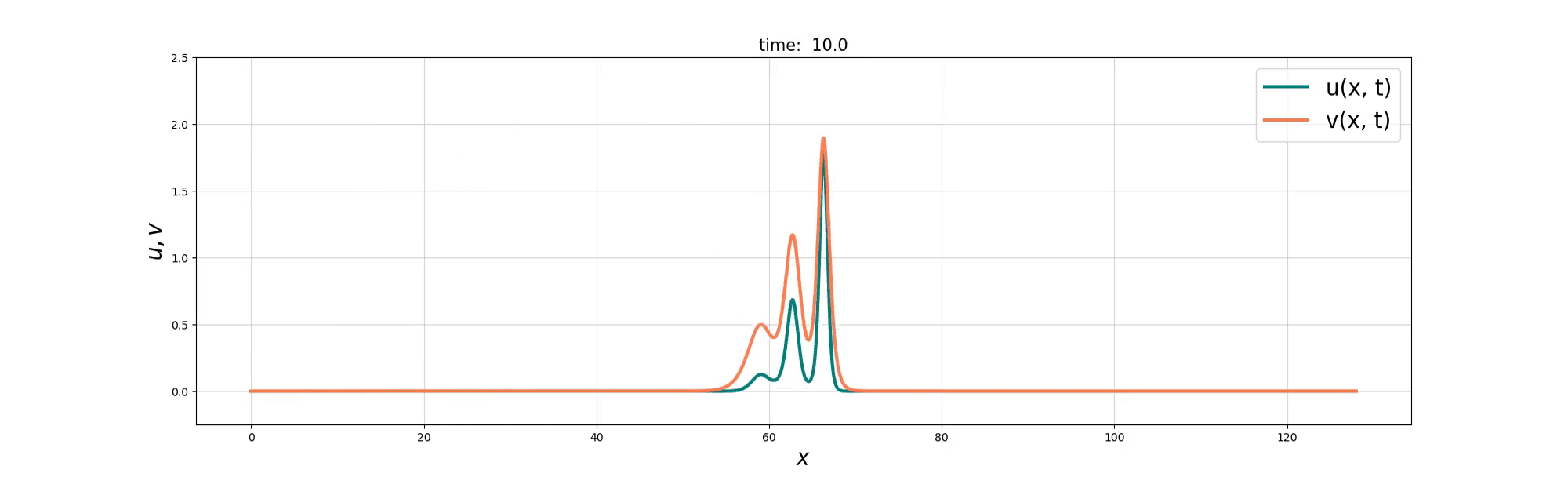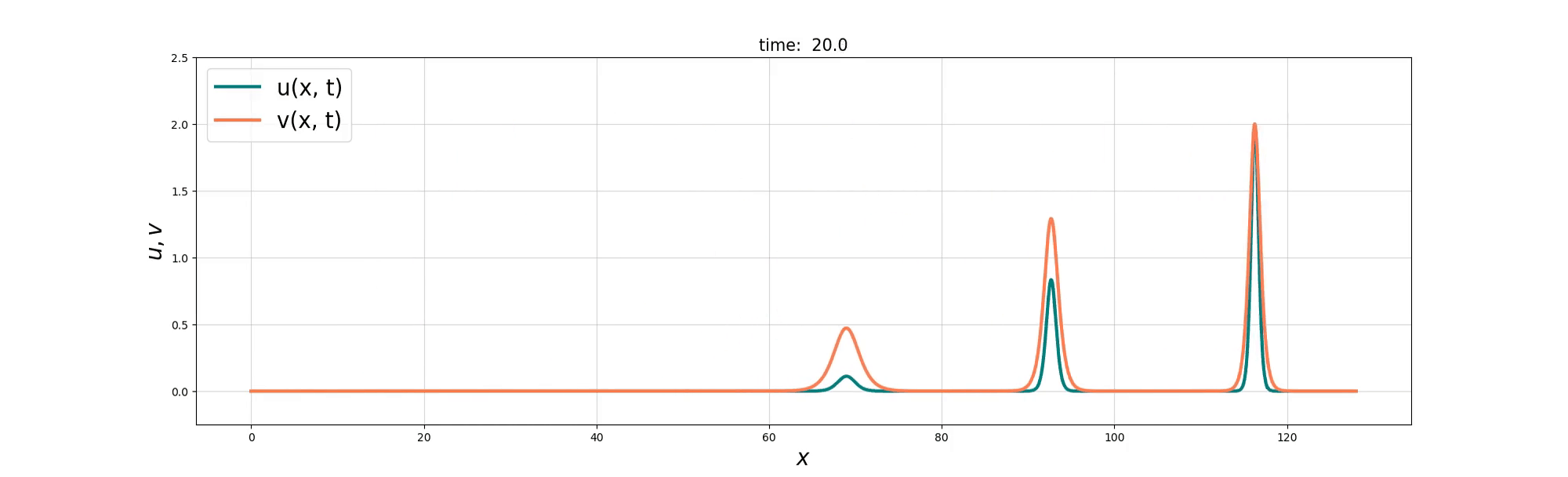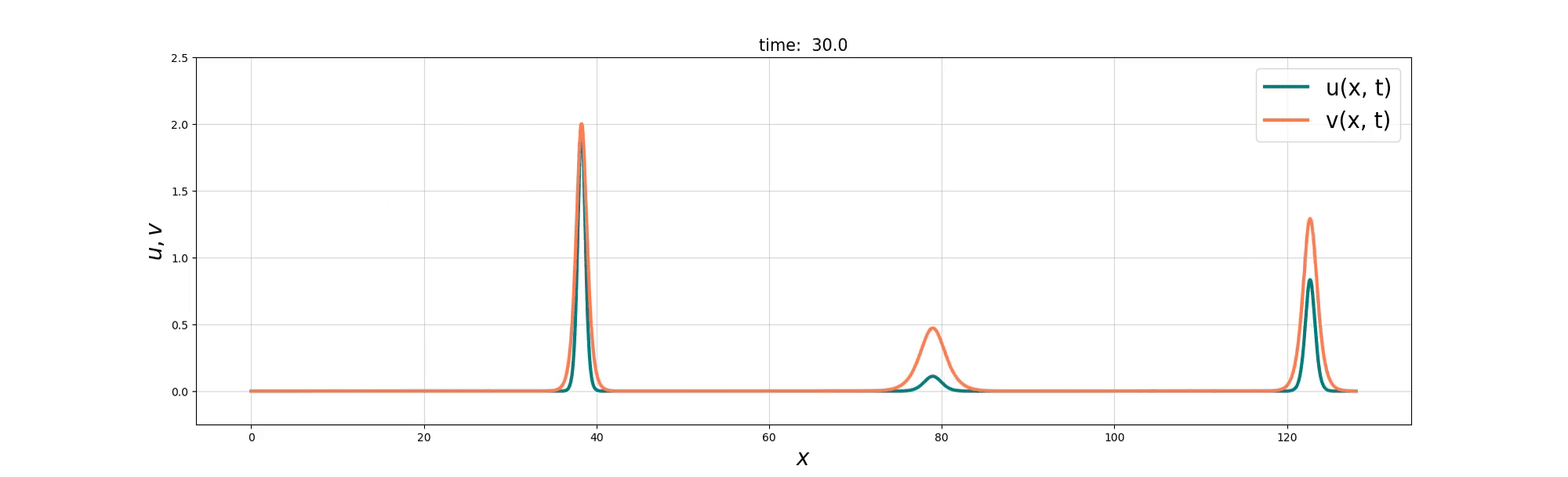
Soliton and Bore interaction

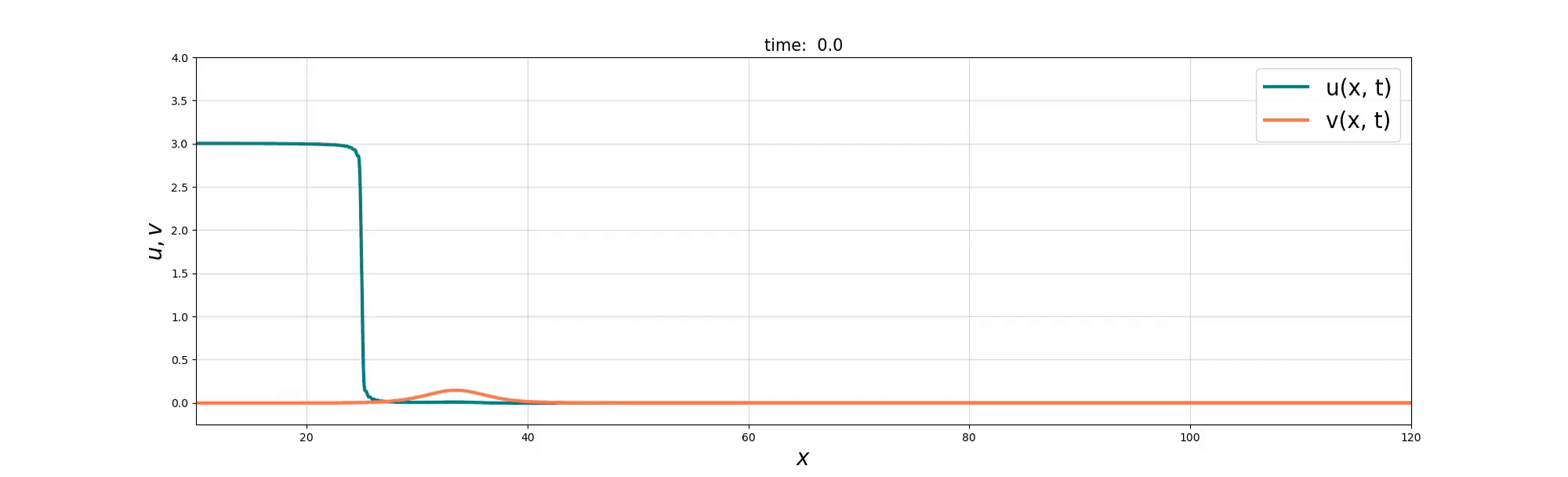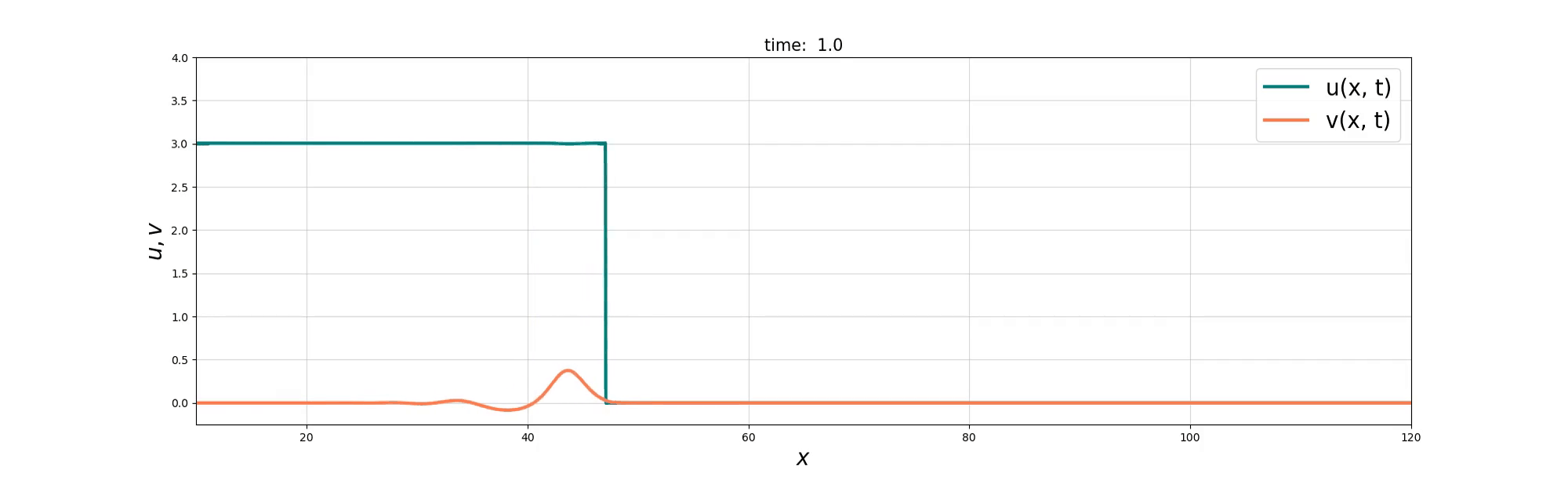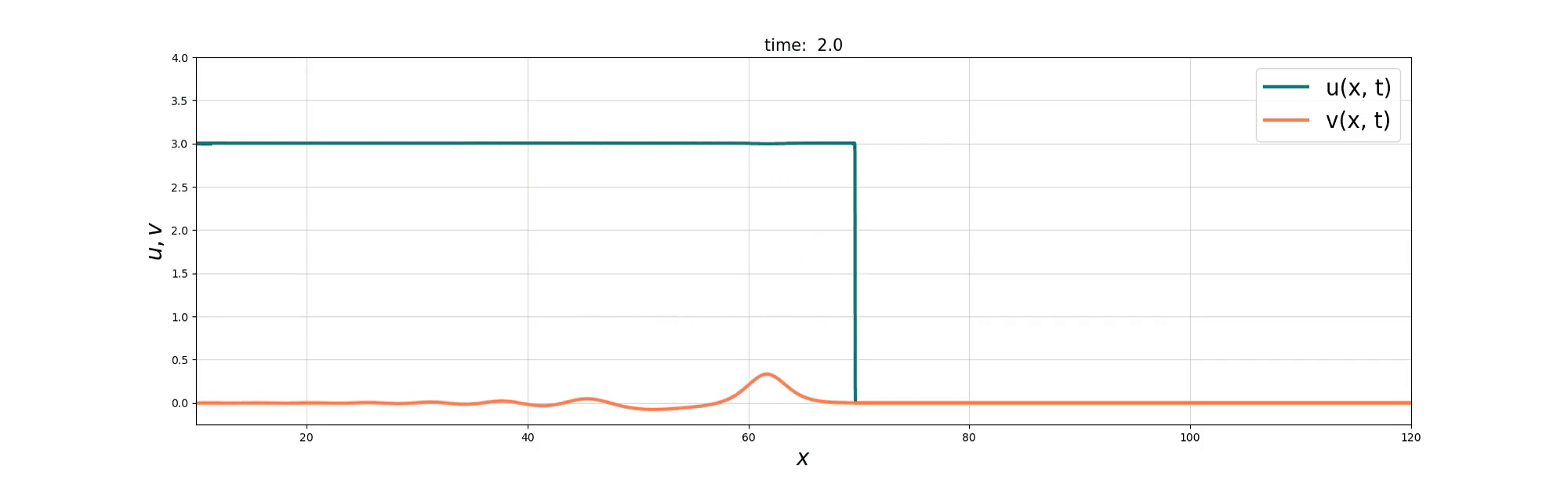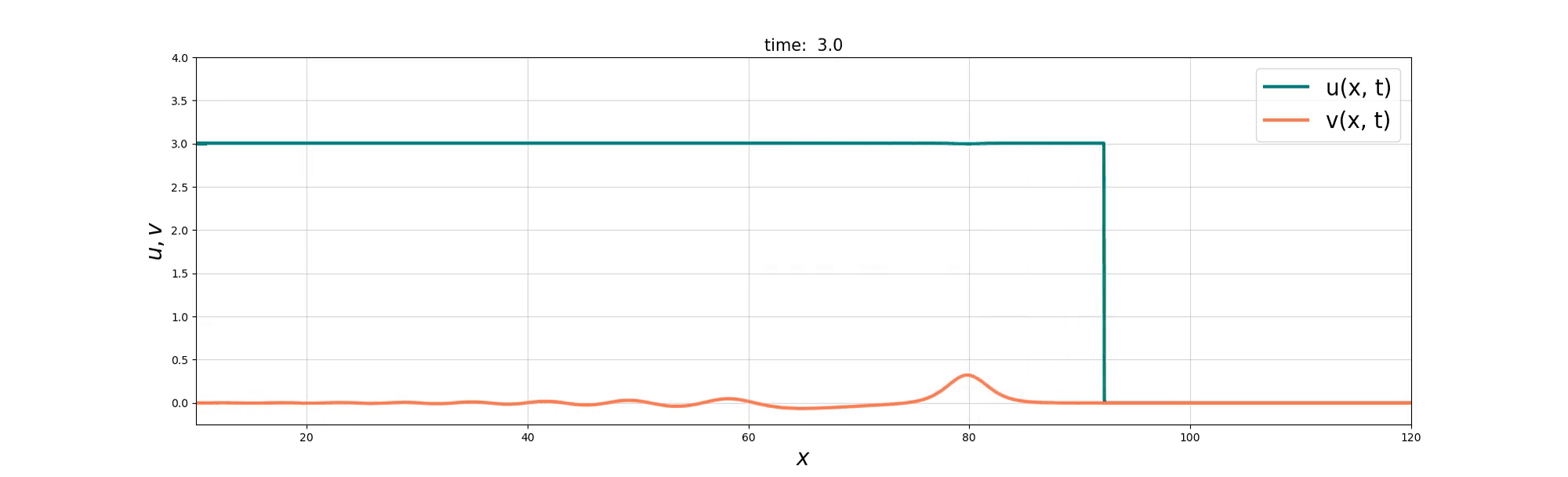
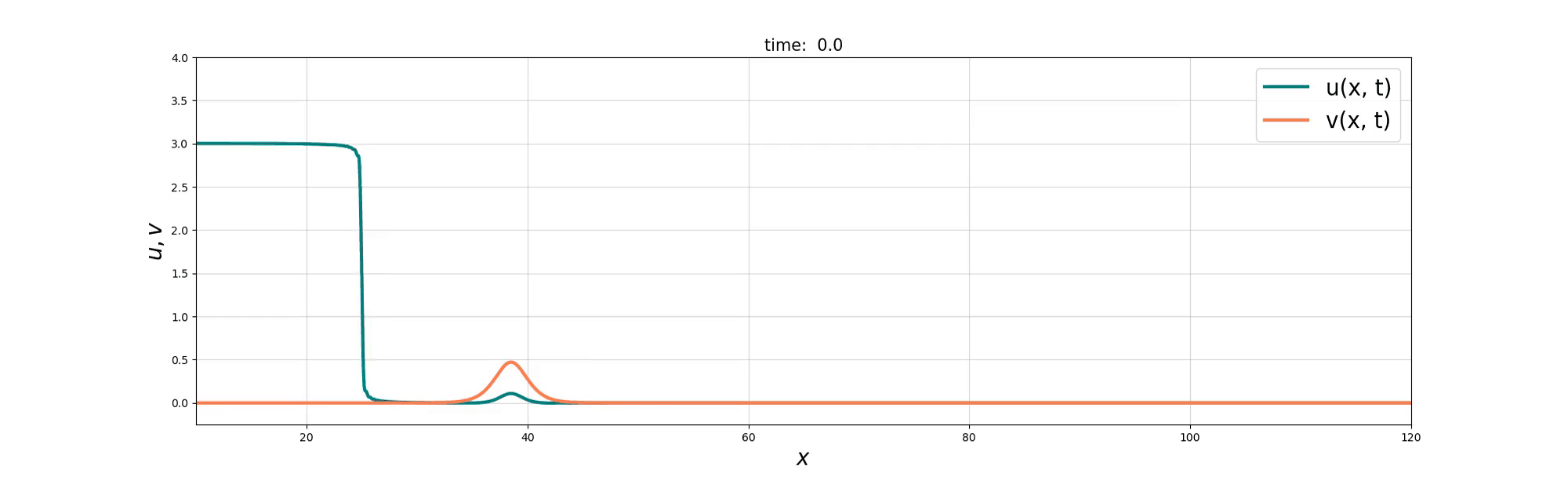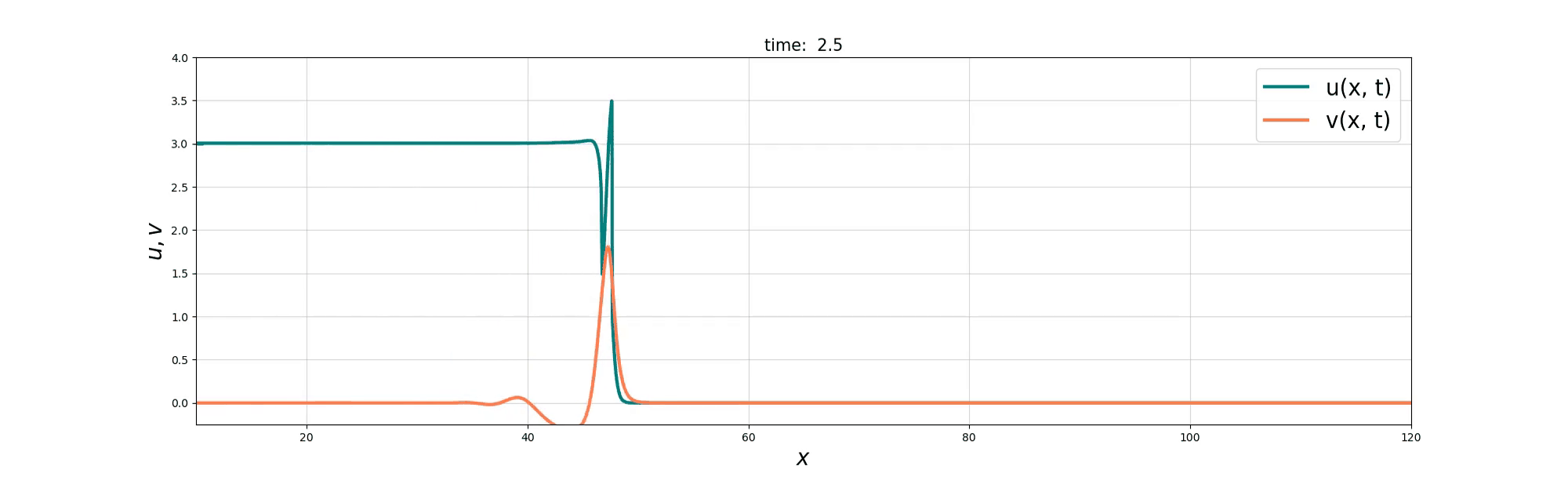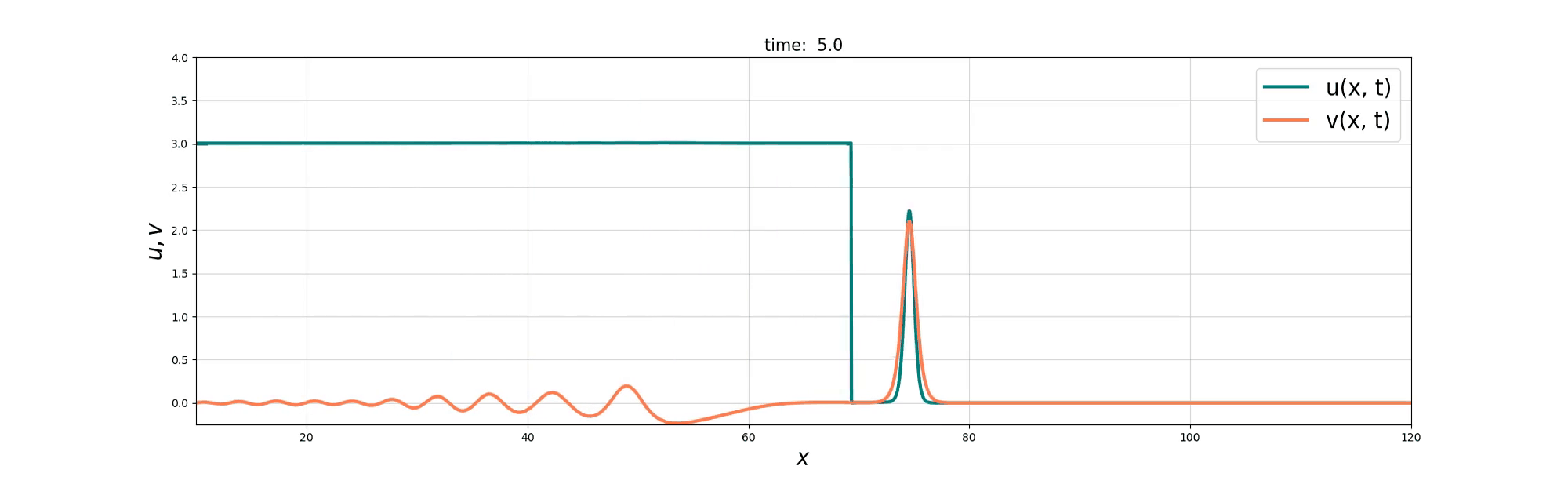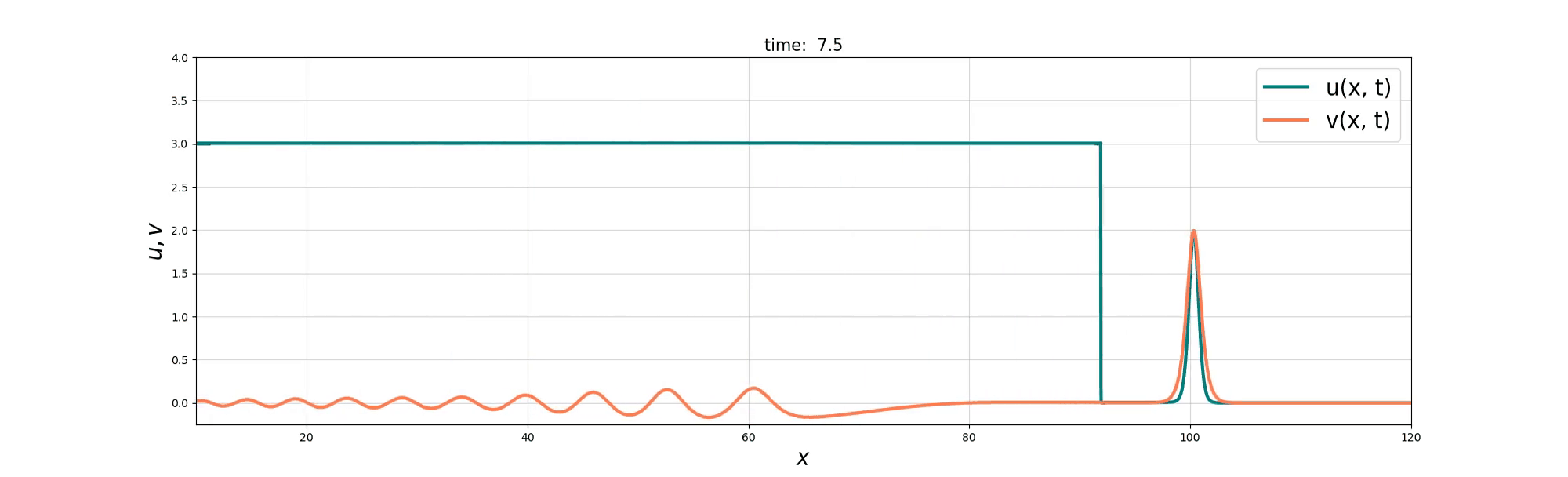
Soliton Fusion